網站導航
鐵芯電抗器直流偏磁仿真驗證
作者:威博特鐵芯 發布時間:2019-03-30 15:01:18 瀏覽次數:本仿真在 MATLAB7. 1 的環境下進行,實驗中用的鐵芯電抗器鐵芯為晶粒取向性硅鋼片,這種鐵芯材料的飽和密度大概在 1. 9 ~ 2. 0T。可以查到該型號硅鋼片的磁化曲線 B - H 數據表,再對數據表中的 B- H 數據對進行處理,擬合出 B - H 的函數曲線具體表達式,根據文獻擬合表達式采用:
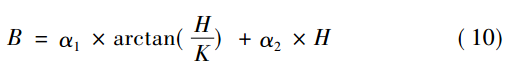
式中 α1、α2、K 為擬合表達式的擬合系數。
利用 MATLAB 中的 cftool 工具得出其擬合系數分別為:
利用 MATLAB 中的 cftool 工具得出其擬合系數分別為:
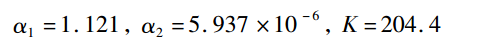
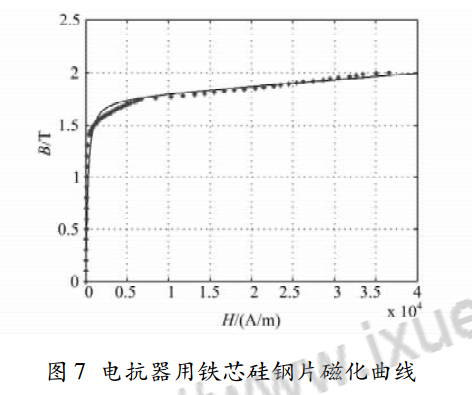
擬合出的磁化曲線如圖 7 所示。可以從圖 7 顯然看出這種鐵芯材料的飽和密度確實大概在 1.9 ~2.0T。得出鐵芯電抗器的鐵芯硅鋼片磁化曲線和磁化曲線具體表達式后,在 MATLAB7. 1 的環境下仿真驗證。
假設 PAPF 逆變器輸出的 a 相電流表達式近似為:
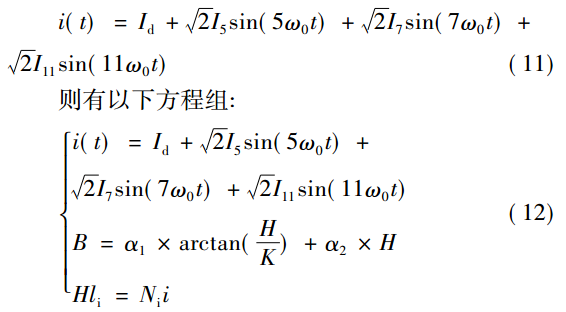
式中 Id 為 PAPF 逆變器輸出的 a 相電流的直流分量;B 為磁感應強度; H 為磁場強度。
上述方程組聯立可以得出磁感應強度 B 與時間 t的函數關系式:
上述方程組聯立可以得出磁感應強度 B 與時間 t的函數關系式:
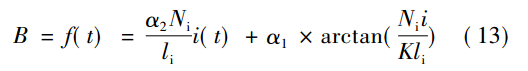
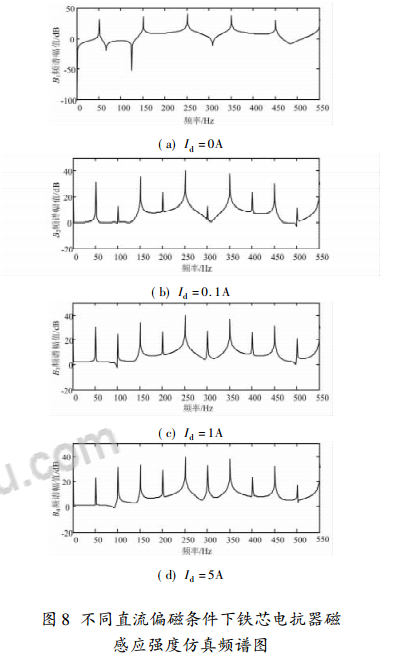
已知 Ni = 500 匝,li = 0. 75m,代入數據得出 B =f( t) 的具體表達式。在 MATLAB7. 1 環境下編寫仿真程序,分別在 Id 為 0A、0. 1A、1A、5A 四種情況下進行仿真,同時對 f( t) 進行 FFT 變換,得出磁感應強度 B仿真頻譜圖如圖 8。
由于磁場感應強度 B 產生感應磁通,進而產生感應電動勢,相應產生感應電流,由電磁感應定律可知,它們的相互關系可以表示為:

由式( 14) 可知,感應電流 i' ( t) 的諧波分量和 B的諧波分量相同。由圖 8( a) 中所示的仿真結果可以看出,當 Id = 0A 時,磁感應強度 B1 主要以 3、5、7 等奇次諧波分量為主,幾乎沒有偶次諧波分量,故感應電流 i1 '( t) 也主要以 3、5、7 等奇次諧波電流為主,偶次諧波電流很小; 但是由圖 8( b) 所示,當 Id = 0. 1A時,磁感應強度 B2 不僅含有 3、5、7 等奇次諧波分量,而且還出現了較大幅值的 2、4、6 等偶次諧波分量,相對應地感應電流 i2 '( t) 中也將會出現較大的偶次諧波分量; 隨著直流分量的增大,如 Id = 1A,Id = 5A 時,偶次諧波幅值進一步增大,其中 2 次諧波增幅大,如圖 8( c) 、( d) 所示。由此可見,圖 8 仿真圖像顯示的結果驗證了 PAPF 輸出濾波器中的鐵芯電抗器直流偏磁產生了額外的偶次諧波,并和有效的諧波補償電流一起注入到電網,直接影響到 PAPF 的濾波性能。





